Sunday, December 22, 2024
Sunday, May 26, 2024
Thursday, October 19, 2023
學習方法論：Inner Game Plus « NickWarm's Blog
通天道的内心艺术 -《网球的内心游戏》
如何改善：即使知道問題卻仍打不好球（遊戲）的困境？（上）
如何改善：即使知道問題卻仍打不好球（遊戲）的困境？（下）
台灣沒有代理這本書，最後我是讀网球的内心游戏(网络拼凑版)這個中國翻譯的版本
一連幾天，一氣呵成讀完，最初的感動紀錄於讀完網球內心遊戲的初步感想。
我內化後推導出的方法論：Inner Game Plus
Inner Game Plus 是我結合Inner Game of tennis與Learning how to learn的方法論，所推導出的學習方法論。
對我來說，非常適合各種youtube教學影片與MOOC當道的現在。
學習順序
1。快速建構組塊，建立世界觀
2。腦中有了初步的世界觀後，才詳讀背後運作的原理
3。Mind Mapping：透過心智圖梳理知識
4。內化成自己的能力：一個時間週期內，間隔錯開不同天，反覆練習
執行細節
[Step.1 建立世界觀]
跳過理論的片段，直接看實戰的部分，例如：數學例題、程式demo範例
把影片聲音關掉，速度調成兩倍
快速瀏覽兩倍速的影片，不熟悉的部分重複刷個三四遍
刷的過程中，有不懂的，疑惑的都不要停，反覆刷，直到範例的操作步驟在你腦中自然形成畫面
停下影片，休息片刻5到10分鐘
自己實際操作，快速手寫數學運算式或coding程式碼，遇到任何bug都不批判不帶任何情感，解掉bug做簡單筆記，然後繼續學習。
1~5步驟稱之為「番茄時鐘工作法」，詳情請見Learning how to learn 初學筆記
在此簡單說一下為何重複刷完影片後要休息。這套學習方法論我實際操練過幾次後發現，快速地重複刷影片這讓你的大腦處於專注模式，而專注力是有限資源、是消耗品，若你一直持續高強度的重複刷兩倍速影片，很快你今日的專注力就會被消耗殆盡，剩下的工作都會效率非常差。所以在此建議，一個範例、一段程式碼在2倍速刷完後，休息片刻讓大腦進入發散模式，然後再繼續。
Inner game of tennis
Learning how to learn
[Step.2 理解背後原理]
反覆操作第一階段的步驟，完成大部份的例題，接著
影片調成正常速度，理解背後的理論與思考脈絡
做筆記
學數學請用手寫筆記本搭配Markdown做筆記，寫程式請全程用Markdown做筆記
數學筆記，第一次寫時，請不要寫得太詳細工整
程式筆記，在專案下開一個markdown檔寫筆記
柿子挑軟的吃
有中文教材就先啃中文，然後才去讀英文教材。
讀不懂沒關係，繼續讀。然後換下一個教材或教學，從不同的角度切入 來學習相同的題目，你會越來越容易理解。
學程式如何做筆記，請參閱臨摹程式如何做筆記
為何學數學時不要寫工整的筆記。詳情請見大學時我讀書的方法
[Step.3 Mind Mapping]
Mind Mapping：透過心智圖梳理知識。
詳情請參閱Learning how to learn筆記：心智圖、xmind使用技巧這兩篇文章。
[Step.4 內化成自己的能力]
以前大學時，臨摹一個新學習的數學範例我也都會重複刷個好幾次，在此推薦更有效率的內化方法「間隔重複」：
一個時間週期內，間隔錯開不同天，反覆練習
詳情請參閱Learning how to learn筆記：間隔重複。
程式的練法，請參考透過Git有效率地練功
理論依據
我個人很推崇Barbara Oakley教授在Coursera所開的Learning how to learn這門課教導的學習方法論，在此謹約略概述
大腦分為專注模式與發散模式，從初學到熟練需要透過專注模式反覆練習，突破性的創意與發明都是在發散模式下達到，詳情請參閱learning how to learn 初學筆記
會覺得學習困難，主要是因為腦中沒足夠的畫面建立學習某專業領域的世界觀。依此邏輯，學一個新領域時，最初的步驟不應該是學習理論，而是大量實戰來建構腦中的基模。有了足夠的基模後，再去學習理論，就有足夠的基模快速建立世界觀。
學習新領域時，由於事事皆新，無法順暢學習於是加深挫折感，也更容易分心，為了要讓學習更有效率與專注，可以採用番茄工作法：以每25分鐘為一組，在25分鐘之內全神貫注學習，時間到了之後就停下來稍作休息。休息是必要的，透過休息的發散模式，讓大腦的記憶更穩固。
為了更有效率的使用大腦，練習應該使用間隔練習，請參閱Learning how to learn筆記：間隔重複。
Barbara Oakley原始的方法論必須要在對理論的理解還不完備前，先透過大量的實戰來建構基模與建立世界觀，但是導入Inner Game的方法論後，我們可以透過重播教學影片，讓範例的邏輯步驟在我們面前反覆演練，直到在腦中形成清晰的畫面。
Inner Game最打動我的地方
書中以網球教學為例
建議教網球時，不要口頭說明講解每一個細節步驟
而是「直接演練」給學習者看
一個動作重複個十遍，不帶指示不講細節，讓學習者「不要思考，專注地看」，接著讓學習者自己實際演練
注意：學習者不要去判斷自己的動作對或錯，就只是把剛剛看到的示範畫面在腦中重現，讓身體自然地依循看過的畫面，然後重現它
Inner Game的核心價值觀
1。拋棄評價
2。用圖像規劃的藝術
3。順其自然的擊球
4。集中注意力
Inner Game 的步驟與細節
在前面的章節Inner Game的核心價值觀之中的拋棄評價，就是拋棄分別心。
Inner Game的中譯「網球的內心遊戲」，裡面很大張篇幅在討論學習者的內心狀態。對岸翻譯的版本，大都採用我1、我2 來代表「在心中對自己下判斷好與壞、對與錯 的邏輯意識」與「負責執行的身體」。
但是對我來說，翻譯文使用我1、我2 這兩者來代表上面那兩個觀念，是非常不直覺。我比較喜歡的是teller與doer。
直接使用英文，會非常直觀。
teller就是「在心中對自己下判斷好與壞、對與錯 的邏輯意識」。
doer就是「負責執行動作的身體」
內心遊戲的學習方法
以下內容引用自网球的内心游戏(网络拼凑版)，也改用teller與doer來代表這兩個狀態。
第一步
觀察現存的行為，不做判斷，
例子：我的最後三個反手落地有些長了，大約有二英尺吧。我的球拍（出拍）有點猶豫，隨揮沒有一直進行到底。也許我應該觀察我的後擺高度„是，是這樣，它大約在我的腰部之上„ 在那裡，那擊球更有節奏，但是它停住了。(以有興趣，有分隔的口氣如上提出。)
第二步
用想像和感覺進行規劃（將結果視覺化）
不要使用命令。邀請doer用執行期望方式來達到預期的結果。把感覺行動和預期的擊球的所有元素利用視覺圖像顯示給doer。如果你希望球去發球區外角，你只要想像球朝向目標的必要道路，然後就像將解決問題一樣將它輸入計算機。不用設法改正錯誤。
第三步
讓它自然發生！相信doer
邀請你的身體來做一個指定的動作，給它自由來做。身體是被信任的，不需要頭腦有意識的控制。發球更像是發球本身。努力doer自發的，不是來自teller的企圖。讓它自然發生不意味去妥協；它意味doer只使用工作必需的肌肉。沒有什麼是強迫的，你的連貫就像江河一樣確定和強大。
第四步
不做評判，冷靜的觀察結果，致連續觀察過程，直到行為自動化
雖然選手知道他的目標，但是他沒有情感地介入它，因此能冷靜地觀看結果並體驗過程。通過這麼做，專注是達到的最好方式，學習以最高的速率進行；只有結果不符合指定的圖像時，才需要重新規劃。否則，只需要對變動的行為進行連續的觀察。觀看它變動；不是做改變。
過程是難以置信的簡單。重要的事是體驗它。不要讓它太理智化。看它感覺象什麼，要求自己做什麼，讓它自然發生，無需刻意的嘗試。對於多數人它是種驚奇的體驗，並且結果他自己會說話。
這個學習方法可以在場內外用很多活動來實踐。你越多讓自己免於在網球場的執行控制，你越能獲得在人體內的美好機制的信心。你越信任它，它就越可勝任。
Inner Game能夠work，背後的原理
讀「網球的內心遊戲」的過程中一直會想到NEW AGE對實相創造的觀點、巴觀的思想、禪，尤其是天地一沙鷗的作者理查巴哈在夢幻飛行這本書裡的思想「順流，順其自然」。
如果要理解為何「圖像規劃」可以讓身體自然而然符合，而不用刻意為之，可以去看這本找回祈禱的力量。
舊書已絕版，再版書名為無量之網 2：正確祈禱，連結萬物為你效力
如果你翻這本書翻幾眼覺得都是屁話，你可以先讀讀該作者的前一本書無量之網，來理解NEW AGE相關的數學與物理是如何運作在真實世界的
舊書已絕版，再版書名為無量之網：連結宇宙萬物的母體
為了吸引你的注意，我們來稍微看一下無量之網這位作者的經歷
桂格．布萊登 Gregg Braden
曾任資深太空電腦系統設計師（Martin Marietta Aerospace）、電腦地質師（菲利普石油公司）及技術操作經理（思科）
人生前半部的工作都是極度邏輯的資深工程師，為何會開始探討NEW AGE這種形而上學的領域呢，你不好奇嗎？
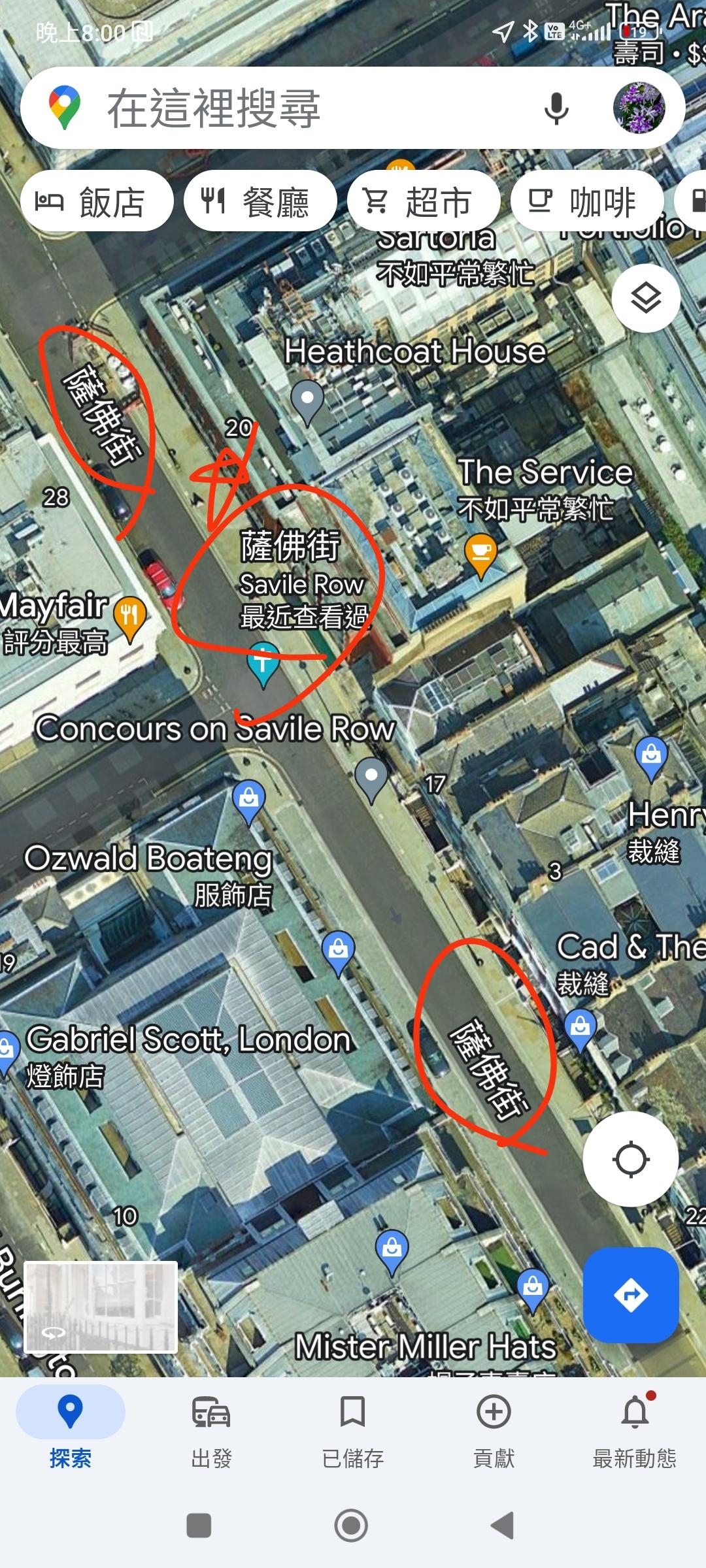
西米羅，西裝，Savile Row street
青蚵仔嫂中＂別人的阿君仔是穿西米羅＂ 這西米羅是什麼？原來西米羅的原文是 Savile Row，是一條街道的名稱，這條街是倫敦一條以精工客制西裝而聞名的街道 Savile Row Street（西米羅街）。所以穿西米羅就是穿手工精製的西裝的意思。猜想它是透過日語在台灣民間流傳開來的。
西裝專家指出，「西米羅」不是日語，而是英文，但是原文並不是指西裝，而是一條街道的名稱，這條街道就是Savile Row Street（西米羅街）是倫敦一條很有名的街，而且是高級西裝一條街，有超過250年的歷史！
日本西化之後，學習西方穿西裝，上層社會更認為只有來自英國倫敦Savile Row的西裝，才算真正的西裝，於是Savile Row（西米羅）漸漸就變成西裝的代名詞了。日本統治台灣五十年，台灣民眾跟著日本人穿西裝，還以為西米羅的意思就是西裝。
日本統治時期，許多台灣知識分子都穿西裝， 這是因為當時如果穿著清朝傳統服裝，很容易會被認為是底層的勞動階級，買不起西裝，或是心向清國，不服日本。 皇民化運動推行之後，日本總督府嚴格規定不許穿中式服裝，尤其是有布扣的衣服，一經「大人」發現，還可能當街直接剪毀。
塞維(薩佛)街（英語：Savile Row，/ˌsævɪl ˈroʊ/）是一個在倫敦中央梅費爾的購物街區，因為傳統的客製男士服裝行業而聞名。塞維街的重要性從17世紀便開始醞釀，在當時代表了歐洲皇家貴冑信賴與炫耀個人財富品味的地方。 塞維街位於的梅費爾區至今是全球最昂貴的地段之一。[1] 量身訂製(Bespoke) 這個專有名詞便是源於這得天獨厚的環境，這條充滿傳奇的短街被稱為「西裝裁縫業的黃金道」，[2]來這裡光顧過的客人包括溫斯頓·邱吉爾、納爾遜勳爵以及拿破崙三世。
聽了一輩子西米羅，倫敦薩佛街，塞維街
塞維街Savile Row Street - 維基百科，自由的百科全書https://zh.wikipedia.org/zh-tw/%E8%96%A9%E4%BD%9B%E8%A1%97
/mwchuang
Friday, January 8, 2021
Sunday, September 8, 2019
也談數學“黑洞”——關於卡普雷卡爾常數 金彈子 (原創)
也談數學“黑洞”——關於卡普雷卡爾常數 金彈子 (原創) http://blog.sina.com.cn/s/blog_4d0579fe01000955.html
美國數學教授Michael W Ecker在《數學“黑洞”》一文中對卡普雷卡爾常數(Kaprekar,s constant)描述道：取任何一個4位數（4個數字均為同一個數字的例外），將組成該數的4個數字重新組合成可能的最大數和可能的最小數，再將兩者的差求出來；對此差值重複同樣的過程（例如：開始時取數8028，最大的重新組合數為8820，最小的為0288，二者的差8532。重複上述過程得出8532－2358＝6174），最後總是達到卡普雷卡爾黑洞：6174。 （見美國《新科學家》，1992，12，19，p38。中國《參考消息》，1993，3，14-17）
稱之“黑洞”是指再繼續運算，都重複這個數，“逃”不出去。
但是，4位數以外的其它位數的數有沒有“黑洞”？如果有,它們之間有沒有什麼規律性？還有沒有其它更多的內容? 《數學“黑洞”》沒有說到。本文就是對這些進行討論。
我在這裡把以上計算得出卡普雷卡爾常數的過程簡稱運算，這個現象稱歸斂，其結果6174稱歸斂結果。以下討論，限於自然數（正整數）。
一、 4位數以外的其它位(任意位)的數的歸斂
舉一些位數的數的運算結果如下：
例1－1 如卡氏常數所述，所有的4位數經運算都歸斂到6174。
例1－2 所有7位數經運算都歸斂到數組
8，429，652
7，619，733
8，439，552
7，509，843
9，529，641
8，719，722
8，649，432
7，519，743
例1—3 所有10位數經運算都歸斂到以下2個數和5個數組：
2個數是: 1) 9，753，086，421
2) 6，333，176，664
5個數組是:
1)
8，655，264，432
6，431，088，654
8，732，087，622
2)
6，433，086，654
8，332，087，662
8，653，266，432
3)
8，765，264，322
6, 543,086, 544
9，751，088，421
4)
9，775，084，221
9，755，084，421
8，321，088，762
5)
8，633，086，632
8，633，266，632
6，433，266，654
4，332，087，666
8，533，176，642
7，533，086，643
8，433，086，652
此外:
一位數的歸斂數是0(沒有意義)。
二位數的歸斂數是9，但已不是2位數。以後的討論均不含它們。
三位數的歸斂數是495，其特殊性後面述及。
通過運算知道，任意n位的數經運算後都能歸斂到三類結果，可能是一個數（稱歸斂數），或是一個數組（稱歸斂組），或若干個數和數組兼而有之。少數歸斂結果是唯一的，如3位數、4位數、7位數，其它則不是唯一的，但其個數是可以確定的有限個數。得到歸斂結果以後，繼續運算也是“逃”不出這些歸斂結果的。任意n位的數各位數字相同時(各有9個)，運算結果為0。可視0為它們的特殊歸斂結果,這個歸斂結果沒有意義。這個結論是本文最重要的結論之一。
要計算任意n位數的歸斂結果，理論上必須對該n位數的所有數進行運算，實際上不可能也沒有必要。分析可知，只須少量運算即可得出。例如：
5位數不必運算9×104 個數(10的4次方)，只須運算54個數。
10位數不必運算9×109 個數(10的9次方)，只須運算2001個數。
17位數不必運算9×1016個數(10的16次方)，只須運算48，049個數（或更少）。等等。
二、 歸斂結果之間的聯繫和派生現象
歸斂結果之間是互相有相關關係的.
1．聯繫位數較少的n位數的歸斂結果可按一定規律嵌入一些特定的數字（以下用黑體字表示）後，派生成位數較多的N位數（N＞n）的歸斂結果。原n位數的歸斂結果稱N位的數根。
用符號К跟在嵌入數後，表示嵌入К個相同的數。如3К表示嵌入К個3，當К＝5，表示嵌入5個3：33333。 К為≥0的任意整數。舉例如下。
第一類 歸斂數派生歸斂數
例2—1—1
4位歸斂數 6174 逐次嵌入3和6這2個數，分別得到6位、8位……的歸斂數。
6位： 6 3 17 6 4，
8位： 6 33 17 66 4，
……
N位： 6 3К 17 6К 4 N＝4＋2К
6174 稱為它們的數根.
例2—1—2 8位歸斂數 97，508，421 逐次嵌入 9和 0 這 2個數，分別得到 10位、12位…… 的歸斂數。
10位： 9，9 75，084，2 0 1
12位： 9 99，750，842，00 1
……
N位： 9 9К 750842 0К 1 N＝8＋2К
97，508，421 稱為它們的數根.
例2—1—3 8位歸斂數97，508，421逐次嵌入7，2、5，4、1，8這6個數後分別得到14位、20位…… 的歸斂數。
14位： 97，7 5 5，1 08，8 4 4，2 21
20位：97，77 5，55 1，1 08，88 4，4 4 2，2 21
……
N位： 97 7К 5 5К 1К 08 8К 4К 4 2К 21
N＝8＋6К
97，508，421 稱為它們的數根.
例2—1—4 17位歸斂數98，765，420，987，543，211逐次嵌入8，6，4，2，9，7，5，3，1這9個數後分別得到26位、35位…… 的歸斂數。
26位： 98，876，654，422，099，877，554，332，111
35位：98，887，666，544，4 2 2，2 09，99 8，777，555，433，321，111
……
N位：98 8К 76 6К 54 4К 2 2К 09 9К 8 7К 7 5К 54 3К 32 1К 11
N＝17＋9К
98，765，420，987，543，211稱為它們的數根.
例2—1—5 3位歸斂數495逐次嵌入5，9，4（僅第一次嵌入略不同，後述）後，分別得到6位、9位…… 的歸斂數。
6位： 549,94 5 (第一次嵌入略不同)
9位： 5 5 4，9 99，44 5
……
N位： 5 5К 49 9К 4К 5 N＝3＋3К
549,945稱為它們的數根.
第二類 由歸斂數派生歸斂
例2—2—1 8位歸斂數97，508，421分別逐次嵌入數組
7，2
5，4
1，8
後，分別得到10位、12位…… 的歸斂組（注：嵌入形式有別於例2—1—3）。
10位：
9，7 7 5，084，2 21
9，75 5，08 4，421
9，751，08 8，421
12位：
97 7，7 50，84 2，2 21
975，55 0，8 44，421
975，11 0，8 88，421
……
N位：
97 7К 5084 2К 21
975 5К 08 4К 421
975 1К 08 8К 421
N＝8+2К
97，508，421稱為它們的數根.
第三類 由歸斂組派生歸斂組
例2—3—1 8位數歸斂組
86，526，432
64，308，654
83，208，762
各數對應逐次嵌加數組
5，4
1, 8
7，2
後分別得到10位、12位…的歸斂組。
10位：
8，65 5，26 4，432
6，43 1，08 8，654
8，7 32，087，6 2 2
12位：
865，55 2，6 44，432
643，11 0，8 88，654
877，320，876，22 2
N位：
865 5К 26 4К 432
643 1К 08 8К 654
8 7К 320876 2К 2
……
N＝8＋2К
原8位數歸斂組
86，526，432
64，308，654
83，208，762
就稱為它們的數根.
例2—3—2 11位歸斂組
96，641，975，331
88，431，976，512
87，641，975，322
86，541，975，432
86，420，987，532
各數分別逐次嵌入8，6，4，2，9，7，5，3，1這9個數後分別得到20位、29位、38位…… 的歸斂組。
20位
98，666，44 2，19 9，7 75，5 3 3，31 1
88，864，4 32，19 9，7 76，5 53，1 12
8 8，76 6，4 4 2，19 9，7 75，53 3，212
8 8，6 6 5，4 42，19 9，7 75，54 3，31 2
8 8，6 6 4，4 2 2，09 9，8 7 7，5 5 3，3 1 2
……
N位:
9 8К 66 6К 4 4К 2К 19 9К 7 7К 5К 5 3К 33 1К 1
88 8К 6К 4 4К 3 2К 19 9К 7 7К 6 5К 5 3К 1К 12
8 8К 76 6К 4 4К 2К 19 9К 7 7К 5К 5 3К 32 1К 2
8 8К 6 6К 54 4К 2К 19 9К 7 7К 5К 54 3К 3 1К
8 8К 6 6К 4 4К 2 2К 09 9К 8 7К 7 5К 5 3К 3 1К 2
N＝11＋9К
原11位歸斂組
96，641，975，331
88，431，976，512
87，641，975，322
86，541，975，432
86，420，987，532
就稱為它們的數根.
第四類 由歸斂組派生歸斂數
例3—1—4 17位歸斂組
97，665，420，，987，543，321
98，654，320，987，654，311
98，764，320，987，653，211
98，765，431，976，543，211
88，754，320，987，654，212
這歸斂組5個數中任何一個數嵌入(7，2)、(5，4)、(1，8)當中的任何一個數對，經運算後均得到19位歸斂數9，876， 543，209，876，543，211。繼續嵌加，則又成為前述第二類派生。
2. 基礎數根
由上述可知,任意N位數的歸斂結果都是較少n位數的歸斂結果嵌加某些數派生而成（即如前述），因此，這些較少n位數的歸斂結果是派生所有任意N位數歸斂結果的基礎，稱它們為基礎數根。這又是本文的重要結論之一。
它們是以下8個：
1） n＝4 6，174
2） n＝6 549，945
3） ( n＝6 )數組
860，832
862，632
642，654
420，876
851，742
750，843
840，852
4） n＝8 97，508，421
5） (n＝8 )數組
86，526，432
64，308，654
83，208，762
6） n＝9 864，197，532
7） n＝11 數組
86，420，987，532
96，641，975，331
88，431，976，512
87，641，975，322
86，541，975，432
8） n＝13 數組
8，733，209，876，622
9，665，429，654，331
3．層狀組數結構
從歸斂結果可以看出，它們形成了有規律的層狀組數結構。
把奇位歸斂數的中間那個數稱中位數，偶位的中間那兩個數稱中位數，中位數的前段數字稱前段，後段數字稱後段。
中位數前、後相同位數上的兩個數稱數層，兩數之和稱層和。層和為8的層及其包容的所有數稱數核。層和為9的層稱普通層。唯有最外層的層和為10，稱飽和層。
例如 864，197，532 : 是9位數，屬奇位。 9稱中位數；197稱數核，864稱前段，532稱後段；(8，2)稱飽和層，(6，3)、(4，5)稱普通層。
9，975，084，201 : 是10位數，屬偶位。 08稱中位數；08又稱數核。 9975稱前段，4201稱後段；(9，1)稱飽和層，(9，0)、(7，2)、(5，4)稱普通層。
555，499，994，445 : 是12位，屬偶位。 99為中位數；499994稱數核。 555稱前段，445稱後段；(5，5)稱飽和層，(5，4)、(5，4)稱普通層。
總之，所有的歸斂結果都呈層狀組數結構。唯有3位歸斂數495和5位數歸斂組之一的
59，994
53，995
尚未形成完整的層狀組數結構。
4．派生歸斂結果的嵌數規律
（1）嵌入數 嵌入的數是特定的，共有3類。
第一類是數對型，有兩對： 1）9，0 2）3，6
第二類是數組型，有一組：
7，2
5，4
1，8
第三類是數字型，有兩個：
1） 5 9 4
2） 8 6 4 2 9 7 5 3 1
（2）嵌入方法
1）嵌入數的一部分嵌入前段中大於或等於嵌入數的最末一個數字的後鄰位置。另一部分嵌入後段相應位置_____使與嵌入前段的數形成層狀組數結構。
數對型：(9,0)、(3,6)的奇數9，3嵌入前段，偶數0，6嵌入後段。見例2—1—1， 2—1—2。
數組型： 7,2
5,4
1,8
的奇數7，5，1嵌入前段，偶數2，4，8嵌入後段。見例2—1—3， 2—2—1。
數字型：9嵌入數核，8642分開嵌入前段，7531分開嵌入後段。見例2—1—4，2—3—2。
594只能嵌入n＝3＋3К 這類數。 9嵌入數核，5嵌入前段，4嵌入後段。見例2—1—5。
2）飽和層外不能嵌加。 3位歸斂數的最外層層和為9，尚未 “飽和”，視為可嵌加，如例2—1—5。嵌加一次成6位數，最外層飽和了，以後則按上述規律派生。所以本文把549945而不是495作為基礎數根。
3）(9，0)、(3，6)兩對數可以獨對、兩對嵌入或與數組型、數字型組合嵌入。
4）數組
7，2
5，4
1，8
必須“配套”嵌入並按順序:
(7，2)→(5，4)→(1，8)
或 (5，4)→(1，8)→(7，2)
或 (1,8) →(7,2) →(5,4)。
以8位數歸斂組
86，526，432
64，308，654
83，208，762
為例說明。
A，各數均可嵌入（3，6）К，得n＝8＋2К位數的歸斂組。
865 3К 26 6К 432
643 3К 08 6К 654
83 3К 2087 6К 62
B, 各數可對應嵌入
(7，2) К
(5，4 )К，
(1，8) К
得n＝8＋2К位數的歸斂組。
8 7К 652643 2К 2
6 5К 430865 4К 4
832 1К 08 8
歸斂結果之間是互相有相關關係的.
1．聯繫位數較少的n位數的歸斂結果可按一定規律嵌入一些特定的數字（以下用黑體字表示）後，派生成位數較多的N位數（N＞n）的歸斂結果。原n位數的歸斂結果稱N位的數根。
用符號К跟在嵌入數後，表示嵌入К個相同的數。如3К表示嵌入К個3，當К＝5，表示嵌入5個3：33333。 К為≥0的任意整數。舉例如下。
第一類 歸斂數派生歸斂數
例2—1—1
4位歸斂數 6174 逐次嵌入3和6這2個數，分別得到6位、8位……的歸斂數。
6位： 6 3 17 6 4，
8位： 6 33 17 66 4，
……
N位： 6 3К 17 6К 4 N＝4＋2К
6174 稱為它們的數根.
例2—1—2 8位歸斂數 97，508，421 逐次嵌入 9和 0 這 2個數，分別得到 10位、12位…… 的歸斂數。
10位： 9，9 75，084，2 0 1
12位： 9 99，750，842，00 1
……
N位： 9 9К 750842 0К 1 N＝8＋2К
97，508，421 稱為它們的數根.
例2—1—3 8位歸斂數97，508，421逐次嵌入7，2、5，4、1，8這6個數後分別得到14位、20位…… 的歸斂數。
14位： 97，7 5 5，1 08，8 4 4，2 21
20位：97，77 5，55 1，1 08，88 4，4 4 2，2 21
……
N位： 97 7К 5 5К 1К 08 8К 4К 4 2К 21
N＝8＋6К
97，508，421 稱為它們的數根.
例2—1—4 17位歸斂數98，765，420，987，543，211逐次嵌入8，6，4，2，9，7，5，3，1這9個數後分別得到26位、35位…… 的歸斂數。
26位： 98，876，654，422，099，877，554，332，111
35位：98，887，666，544，4 2 2，2 09，99 8，777，555，433，321，111
……
N位：98 8К 76 6К 54 4К 2 2К 09 9К 8 7К 7 5К 54 3К 32 1К 11
N＝17＋9К
98，765，420，987，543，211稱為它們的數根.
例2—1—5 3位歸斂數495逐次嵌入5，9，4（僅第一次嵌入略不同，後述）後，分別得到6位、9位…… 的歸斂數。
6位： 549,94 5 (第一次嵌入略不同)
9位： 5 5 4，9 99，44 5
……
N位： 5 5К 49 9К 4К 5 N＝3＋3К
549,945稱為它們的數根.
第二類 由歸斂數派生歸斂
例2—2—1 8位歸斂數97，508，421分別逐次嵌入數組
7，2
5，4
1，8
後，分別得到10位、12位…… 的歸斂組（注：嵌入形式有別於例2—1—3）。
10位：
9，7 7 5，084，2 21
9，75 5，08 4，421
9，751，08 8，421
12位：
97 7，7 50，84 2，2 21
975，55 0，8 44，421
975，11 0，8 88，421
……
N位：
97 7К 5084 2К 21
975 5К 08 4К 421
975 1К 08 8К 421
N＝8+2К
97，508，421稱為它們的數根.
第三類 由歸斂組派生歸斂組
例2—3—1 8位數歸斂組
86，526，432
64，308，654
83，208，762
各數對應逐次嵌加數組
5，4
1, 8
7，2
後分別得到10位、12位…的歸斂組。
10位：
8，65 5，26 4，432
6，43 1，08 8，654
8，7 32，087，6 2 2
12位：
865，55 2，6 44，432
643，11 0，8 88，654
877，320，876，22 2
N位：
865 5К 26 4К 432
643 1К 08 8К 654
8 7К 320876 2К 2
……
N＝8＋2К
原8位數歸斂組
86，526，432
64，308，654
83，208，762
就稱為它們的數根.
例2—3—2 11位歸斂組
96，641，975，331
88，431，976，512
87，641，975，322
86，541，975，432
86，420，987，532
各數分別逐次嵌入8，6，4，2，9，7，5，3，1這9個數後分別得到20位、29位、38位…… 的歸斂組。
20位
98，666，44 2，19 9，7 75，5 3 3，31 1
88，864，4 32，19 9，7 76，5 53，1 12
8 8，76 6，4 4 2，19 9，7 75，53 3，212
8 8，6 6 5，4 42，19 9，7 75，54 3，31 2
8 8，6 6 4，4 2 2，09 9，8 7 7，5 5 3，3 1 2
……
N位:
9 8К 66 6К 4 4К 2К 19 9К 7 7К 5К 5 3К 33 1К 1
88 8К 6К 4 4К 3 2К 19 9К 7 7К 6 5К 5 3К 1К 12
8 8К 76 6К 4 4К 2К 19 9К 7 7К 5К 5 3К 32 1К 2
8 8К 6 6К 54 4К 2К 19 9К 7 7К 5К 54 3К 3 1К
8 8К 6 6К 4 4К 2 2К 09 9К 8 7К 7 5К 5 3К 3 1К 2
N＝11＋9К
原11位歸斂組
96，641，975，331
88，431，976，512
87，641，975，322
86，541，975，432
86，420，987，532
就稱為它們的數根.
第四類 由歸斂組派生歸斂數
例3—1—4 17位歸斂組
97，665，420，，987，543，321
98，654，320，987，654，311
98，764，320，987，653，211
98，765，431，976，543，211
88，754，320，987，654，212
這歸斂組5個數中任何一個數嵌入(7，2)、(5，4)、(1，8)當中的任何一個數對，經運算後均得到19位歸斂數9，876， 543，209，876，543，211。繼續嵌加，則又成為前述第二類派生。
2. 基礎數根
由上述可知,任意N位數的歸斂結果都是較少n位數的歸斂結果嵌加某些數派生而成（即如前述），因此，這些較少n位數的歸斂結果是派生所有任意N位數歸斂結果的基礎，稱它們為基礎數根。這又是本文的重要結論之一。
它們是以下8個：
1） n＝4 6，174
2） n＝6 549，945
3） ( n＝6 )數組
860，832
862，632
642，654
420，876
851，742
750，843
840，852
4） n＝8 97，508，421
5） (n＝8 )數組
86，526，432
64，308，654
83，208，762
6） n＝9 864，197，532
7） n＝11 數組
86，420，987，532
96，641，975，331
88，431，976，512
87，641，975，322
86，541，975，432
8） n＝13 數組
8，733，209，876，622
9，665，429，654，331
3．層狀組數結構
從歸斂結果可以看出，它們形成了有規律的層狀組數結構。
把奇位歸斂數的中間那個數稱中位數，偶位的中間那兩個數稱中位數，中位數的前段數字稱前段，後段數字稱後段。
中位數前、後相同位數上的兩個數稱數層，兩數之和稱層和。層和為8的層及其包容的所有數稱數核。層和為9的層稱普通層。唯有最外層的層和為10，稱飽和層。
例如 864，197，532 : 是9位數，屬奇位。 9稱中位數；197稱數核，864稱前段，532稱後段；(8，2)稱飽和層，(6，3)、(4，5)稱普通層。
9，975，084，201 : 是10位數，屬偶位。 08稱中位數；08又稱數核。 9975稱前段，4201稱後段；(9，1)稱飽和層，(9，0)、(7，2)、(5，4)稱普通層。
555，499，994，445 : 是12位，屬偶位。 99為中位數；499994稱數核。 555稱前段，445稱後段；(5，5)稱飽和層，(5，4)、(5，4)稱普通層。
總之，所有的歸斂結果都呈層狀組數結構。唯有3位歸斂數495和5位數歸斂組之一的
59，994
53，995
尚未形成完整的層狀組數結構。
4．派生歸斂結果的嵌數規律
（1）嵌入數 嵌入的數是特定的，共有3類。
第一類是數對型，有兩對： 1）9，0 2）3，6
第二類是數組型，有一組：
7，2
5，4
1，8
第三類是數字型，有兩個：
1） 5 9 4
2） 8 6 4 2 9 7 5 3 1
（2）嵌入方法
1）嵌入數的一部分嵌入前段中大於或等於嵌入數的最末一個數字的後鄰位置。另一部分嵌入後段相應位置_____使與嵌入前段的數形成層狀組數結構。
數對型：(9,0)、(3,6)的奇數9，3嵌入前段，偶數0，6嵌入後段。見例2—1—1， 2—1—2。
數組型： 7,2
5,4
1,8
的奇數7，5，1嵌入前段，偶數2，4，8嵌入後段。見例2—1—3， 2—2—1。
數字型：9嵌入數核，8642分開嵌入前段，7531分開嵌入後段。見例2—1—4，2—3—2。
594只能嵌入n＝3＋3К 這類數。 9嵌入數核，5嵌入前段，4嵌入後段。見例2—1—5。
2）飽和層外不能嵌加。 3位歸斂數的最外層層和為9，尚未 “飽和”，視為可嵌加，如例2—1—5。嵌加一次成6位數，最外層飽和了，以後則按上述規律派生。所以本文把549945而不是495作為基礎數根。
3）(9，0)、(3，6)兩對數可以獨對、兩對嵌入或與數組型、數字型組合嵌入。
4）數組
7，2
5，4
1，8
必須“配套”嵌入並按順序:
(7，2)→(5，4)→(1，8)
或 (5，4)→(1，8)→(7，2)
或 (1,8) →(7,2) →(5,4)。
以8位數歸斂組
86，526，432
64，308，654
83，208，762
為例說明。
A，各數均可嵌入（3，6）К，得n＝8＋2К位數的歸斂組。
865 3К 26 6К 432
643 3К 08 6К 654
83 3К 2087 6К 62
B, 各數可對應嵌入
(7，2) К
(5，4 )К，
(1，8) К
得n＝8＋2К位數的歸斂組。
8 7К 652643 2К 2
6 5К 430865 4К 4
832 1К 08 8
三、 歸斂結果的特點
通過以上的討論，可以總結歸斂結果的特點如下。
1．任意數A，其歸斂結果為B，B和A的位數相同。
2．歸斂結果的各數字之和是9的整數倍。如6174：6＋1＋7＋4＝18＝2×9。
1） 任意奇位數（n＝2k－1）和偶位數（n＝2k）的歸斂結果,其各數字之和均為 （k＋1）×9或k×9。
2）n＝3＋3k 位這類數的歸斂結果，無論奇、偶位數，其各位數字之和均為（2k×9。
3）前後兩段數字都是由大到小順序排列。
4）運算中，一次就能形成層狀組數結構而無論是否已成為歸斂結果。只有極少數例外。例如：任意n位數，其中一位為a，其餘n－1位為b（a≠b）如266…6。
5）同一個歸斂組中各數可按順序遞進交換。例如：
86，526，432
64，308，654
83，208，762，
可為
64，308，654
83，208，762
86，526，432
或為
83，208，762
86，526，432
64，308，654
6）歸斂結果的派生有如下傳遞性。
①簡單傳遞。如嵌加(3，6)、(9，0)、864297531的各種情況。見前述例子。
②順序傳遞。只有嵌加數組 7，2
5，4
1，8
的這一種情況.
傳遞順序是循環的7，2→5，4→1，8。當嵌入7，2，就必然也得到嵌入5，4和1，8的“配套”結果。當嵌入5，4，就必然也得到嵌入1，8和7，2的“配套”結果，等等。其餘類推。見例3—2—1。
③配套傳遞。嵌入
7，2
5，4
1，8
數對時，可分別嵌入一對、兩對、三對，但必須“配套”對應。例如 97，508，421的如下嵌入結果：
975 555 11 08 88 4 444 21
97 77 5 111 08 888 42 2 2 1
97 777 5 55 08 44 4 2 22 2 1
其中，К1＝0，К2＝3，К3＝2，К＝К1＋К2＋К3＝5。
位數N＝8＋2К＝8＋2·5＝18
可記為
97 7К1 5 5К2 1К3 08 8К3 4К2 4 2К121
97 7К3 5 5К1 1К2 08 8К2 4К1 4 2К3 2 1
97 7К2 5 5К3 1К1 08 8К1 4К34 2К2 2 1
④組合傳遞。以上各種傳遞的組合。例如50位歸斂組之一：
99，988，776，655，554，433，333，322，099，877，666，666，554，444，332，211，001
99，988，766，554，433，333，322，111，099，888，877，666，666，554，433，211，001
99，988，777，766，544，333，333，221，099，887，766，666，655，433，222, 211，001
分析可知，它是以n＝8 的 8位數的歸斂數 97，508，421 作為數根，嵌加
(9，0) 2次
（К′＝2），
(3，6)6次（К″＝6），
(864297531) 2次（К′″＝2），
以及數組 7，2（К1＝1）,
5，4（К2＝3）
1，8（К3＝0）。
N＝8＋2×2＋2×6＋9×2＋2×1＋2×3＋2×0＝50（位）。
當然該歸斂組還可以分析為其它的數根和派生。
⑤唯一傳遞。僅有n＝3＋3k類嵌加594的情況。見例2—1—5。
歸斂結果的以上特點可用於運算或者派生結果的設計、檢查、驗證等。
通過以上的討論，可以總結歸斂結果的特點如下。
1．任意數A，其歸斂結果為B，B和A的位數相同。
2．歸斂結果的各數字之和是9的整數倍。如6174：6＋1＋7＋4＝18＝2×9。
1） 任意奇位數（n＝2k－1）和偶位數（n＝2k）的歸斂結果,其各數字之和均為 （k＋1）×9或k×9。
2）n＝3＋3k 位這類數的歸斂結果，無論奇、偶位數，其各位數字之和均為（2k×9。
3）前後兩段數字都是由大到小順序排列。
4）運算中，一次就能形成層狀組數結構而無論是否已成為歸斂結果。只有極少數例外。例如：任意n位數，其中一位為a，其餘n－1位為b（a≠b）如266…6。
5）同一個歸斂組中各數可按順序遞進交換。例如：
86，526，432
64，308，654
83，208，762，
可為
64，308，654
83，208，762
86，526，432
或為
83，208，762
86，526，432
64，308，654
6）歸斂結果的派生有如下傳遞性。
①簡單傳遞。如嵌加(3，6)、(9，0)、864297531的各種情況。見前述例子。
②順序傳遞。只有嵌加數組 7，2
5，4
1，8
的這一種情況.
傳遞順序是循環的7，2→5，4→1，8。當嵌入7，2，就必然也得到嵌入5，4和1，8的“配套”結果。當嵌入5，4，就必然也得到嵌入1，8和7，2的“配套”結果，等等。其餘類推。見例3—2—1。
③配套傳遞。嵌入
7，2
5，4
1，8
數對時，可分別嵌入一對、兩對、三對，但必須“配套”對應。例如 97，508，421的如下嵌入結果：
975 555 11 08 88 4 444 21
97 77 5 111 08 888 42 2 2 1
97 777 5 55 08 44 4 2 22 2 1
其中，К1＝0，К2＝3，К3＝2，К＝К1＋К2＋К3＝5。
位數N＝8＋2К＝8＋2·5＝18
可記為
97 7К1 5 5К2 1К3 08 8К3 4К2 4 2К121
97 7К3 5 5К1 1К2 08 8К2 4К1 4 2К3 2 1
97 7К2 5 5К3 1К1 08 8К1 4К34 2К2 2 1
④組合傳遞。以上各種傳遞的組合。例如50位歸斂組之一：
99，988，776，655，554，433，333，322，099，877，666，666，554，444，332，211，001
99，988，766，554，433，333，322，111，099，888，877，666，666，554，433，211，001
99，988，777，766，544，333，333，221，099，887，766，666，655，433，222, 211，001
分析可知，它是以n＝8 的 8位數的歸斂數 97，508，421 作為數根，嵌加
(9，0) 2次
（К′＝2），
(3，6)6次（К″＝6），
(864297531) 2次（К′″＝2），
以及數組 7，2（К1＝1）,
5，4（К2＝3）
1，8（К3＝0）。
N＝8＋2×2＋2×6＋9×2＋2×1＋2×3＋2×0＝50（位）。
當然該歸斂組還可以分析為其它的數根和派生。
⑤唯一傳遞。僅有n＝3＋3k類嵌加594的情況。見例2—1—5。
歸斂結果的以上特點可用於運算或者派生結果的設計、檢查、驗證等。
例如n＝10時共有9×109個數(10的9次方)，其歸斂結果也為10位，其歸斂結果的那兩個數和三個數組的數必然包羅在這9×109個數(10的9次方)之中，即已“隱藏”其中，運算只不過是把它們找出來。
歸斂有以下幾點是顯而易見的：
1．若干個數字相同而數字的位序不同的數，運算中重新排序必然得到同一個max和同一個min，max－min也就相同，必然歸斂得同一結果。
例如n＝8的9×107個數,其中的一個數12，345，678，它的排列有8﹗ =40320個數，這40320個數運算必然歸斂為同一個結果（max－min＝87654321－12345678的最後歸斂結果）。
2．一些“對稱性”數，會歸斂到同一結果。
例如1,111,000,000排列成的84個數和1,111,110,000排列成的126個共210個數；
3,339,999,999排列成的210個數和3,333,333,999排列成的210個共420個數；
99,911,000，99,922,000，99,933,000…，99,988,000分別排列成的350個共2800個數。它們的max－min分別相同，必然分別歸斂到各自的同一個結果。等等.
3．同一個數，各位分別加1或減1（加、減中不能進位或借位），其max－min相同，也必然歸斂到同一個結果。如6位數的543210，其全排列有6﹗ -5﹗ =600個數，各位加1得到654321，繼續加1得到765432，876543，987654，分別各排列成720個共3480個數。它們必然歸斂到同一個結果（max－min＝530865的最後歸斂結果）。
所有的數的歸斂結果的形成，都是運算中重新排序為max、min及max－min使之逐漸“逼近”、“靠攏”到歸斂結果。
四、 結論
由本文以上的討論，可以提出以下結論：任意n位的數，經過卡普雷卡爾運算都能得到具有前述特點的歸斂結果（形成“黑洞”並“落”入“黑洞”）。
還可以提出如下可能性：
1．在確定數根以後，不經運算就能設計出（即直接派生出）任意指定位數的某些歸斂結果。
2．給出任意位數的歸斂結果，可以推算出其前的較少位數或其後的較多位數的歸斂結果的派生路線、派生結果和數根。
本文以上的討論及其結論，筆者還推及負整數，正、負實小數（排除無限小數），均可適用。
以上討論，運算均獲成功，但尚未嚴密論證。供有興趣者共同探索和指正。
參考文章:
1, 美國《新科學家》，1992，12，19
2, 中國《參考消息》，1993，3，14-17
(注:打字中和數字校核中可能有錯誤,敬請指正)
/mwchuang
Friday, August 23, 2019
11 Steps to Becoming a Successful YouTuber
11 Steps to Becoming a Successful YouTuber
how to become a successful youtuberhow to become a successful youtuber
There seems to be a consensus that starting a YouTube channel is no longer ‘worth it’ due to the fact that all of the millionaires have already been born out of the platform. Yes, it’s true that you have a better chance of making “fetch” happen than becoming an overnight YouTube sensation, but that doesn’t mean you can’t have your cake and eat it too. The success of YouTube influencers of the past have made marketers shift how they can potentially reach their audience, so it’s actually a very relevant dream to have for your own channel. The video platform has weaved itself into the marketing fold of many businesses or really anyone looking to share their voice with the world.
Here are the 11 steps you need to take in order become a successful YouTuber:
Define what success means to you and remember it
Develop your channel’s goals and content
Map it out
Make sure your channel page is welcoming
Mind your SEO
Be consistent. Be-be consistent
Get to the point
Keep up with your niche
Manage your community like a boss
Spread the word with a killer website
Learn from your analytics
01. Define what success means to you and remember it
Many define success monetarily, but there’s so much more to it than money in the bank. If you make a ton of money doing a job you hate, would you consider yourself successful despite your lack of fulfillment? Success comes in different forms, and it’s up to you to determine where you consider yourself successful. If you define success outside of greenbacks for your YouTube channel, remember that’s what you’re in it for. Whether its a higher view count for your videos, more subscribers, or just an overall increase of engagement across your channel, keep this as your focus, anything else is just bonus.
02. Develop your channel’s goals and content
YouTube is video. There’s a lot of good content, and a ton of terrible content out there. To stand out in this raging sea, obviously you will need to keep paddling and keep your head above water but you need to have a plan to get to shore. Developing your content is the fun part, but it’s also a job. Here, you’re defining your channels’ voice and your content should align with it. Even if it’s just you and your camera, you’re building your brand’s personality. The easiest way to develop your channel is to be yourself. But what if you’re not particularly interesting even though the content you’re producing is? Well, then there’s nothing wrong with being a little “extra” to add some pep to your videos. (Read: a little – you’re going for pep, not obnoxious. Also, always consider your audience.)
You’ll need to decide what type of content you will be offering up on your channel. The range is huge, from how-to videos, to humor, to reviews. Once you choose that, backtrack to see how you can make the videos unique using your brand’s personality. Depending on your channel’s content and niche, you want to make sure you give yourself some wiggle room to cover trending topics in your industry. If some big news breaks out or there’s a subject you know others with similar channels are talking about, don’t hesitate to ride the wave. It’s important to stay relevant. Even if you’re covering the same topics as others, it gives you an opportunity to add your valuable input on a subject.
03. Map it out
Now with your content type secured, make a plan as to how you will not only execute its creation, but everything in this venture. Think of this as a business plan of sorts and return to it every now and then to make sure you’re adhering to the standards that you set up for yourself. You can also treat this part as a checklist of the things you will need in the creation of your YouTube channel, including any and all equipment you will need to produce quality videos. This is also a good time to figure out who else will be involved with the your channel, if anyone. In essence, build a realistic timeline for your posting schedule, gather topics for your content, and make sure you follow this timeline consistently along your journey.
04. Make sure your channel page is welcoming
You know what’s not cute? An incomplete YouTube profile. If you’re trying to make YouTube “happen” for you, be sure to mind your p’s and q’s. Since the medium is a visual one, presentation is key. Your profile photo or logo needs to be set in the correct place and your channel banner image needs to be the correct dimensions. Other things to think about are the style of your video thumbnails. Do they have their own visual style that you will continue to consistently reproduce? To ensure all your elements are in place and are the correct size take a look at our ultimate social media size guide. You’re welcome.
Brunch Boys successful youtubersBrunch Boys successful youtubers
05. Mind your SEO
Properly setting up SEO for your YouTube videos is beyond important. Since you took the time to produce your videos don’t start slacking now. YouTube is a very sophisticated search engine, and people use it a lot to discover new content. Which means that, by choosing the right keywords, you’ll embetter your chance to be found, seen, and enjoyed. If there are videos similar to one you’re looking to create, take a look at the exact words you typed in for the results. Then try a slight variation to see how the results change just so you can see what a word or two of difference can make. Research the keywords you’d like to use, their popularity, and the keywords your competition uses.
06. Be consistent. Be-be consistent
It doesn’t matter how many of these articles about being successful on YouTube you read through, you will always find this one. You must be consistent to see any kind of success. It’s that or hedge your bets on instant viral success. Don’t get me wrong, that would cool, but the viral route is not a guaranteed one in the least bit. No matter what type of content you’re producing, stay consistent with your timing and type. Set a schedule as to when you will release your videos and try to stick to it. Consistently releasing videos on the same day and time not only tells your audience when they can expect your new content, but it gives you a schedule to work with and abide by. Consistency isn’t just about timing. It’s about ensuring steady, on-brand content.
Let’s say you follow a baking channel on YouTube and it’s your go-to source for all things baking, but the latest episode, without explanation, is all about their trip to a monster truck rally. (Really?) The stark contrast in content, especially without warning, is jarring and will leave your loyal viewers confused. If you want to experiment with your content it would be wise to give your audience a heads up first..
07. Get to the point
You know what’s absolutely, completely unnecessary for a YouTube video? A five minute explanation for something you can (and intend to) show your viewer that only takes 30 seconds. Sounds funny when worded like that, right? Unfortunately, this is terribly common. I’m sorry, but people do not have time for you to waste their time, so just get right to it. If you release how-to videos, it’s an absolute must to get to your point as soon as you can. Explain what the video is going to be about and then dive right in. The point of a video is to “show” your viewer something (If they just want to listen, they would listen to a podcast.) Of course, there will be instances where further elaboration or troubleshooting may need to be mentioned, but save that for later in the video. Your audience will thank you.
how to become a successful youtuberhow to become a successful youtuber
08. Keep up with your niche
When presenting (recording) to your audience, you want to be seen as knowledgeable about your industry. This entails staying up with news about your niche and your video making peers. Keeping up with the news and happenings of your industry (including your competition) allows you to make relevant and fresh content for your viewers. By watching your competitions videos you can see the points and opinions they make before you make your own video. Allowing you to follow up with your own counter argument (if you live for drama) or your own spin to keep it unique. This will also help to establish yourself as a “go-to” channel for someone who wants to stay up to date with a certain subject.
09. Manage your community like a boss
If you measure success by subscriber count, your subscribers are basically gold, so be sure to treat them as such. This goes beyond just answering and liking their comments. Community management can be a job of its own. A great way to engage with your community instantly is to host a live stream. Live video is becoming increasingly more popular, as it allows you to interact directly with your viewers and shows a more candid, off the cuff presentation. This platform is also great for hosting Q&As so your audience can get answers to their burning questions right then and there. You can also flip it and ask your viewers to leave questions in the comments which you can then answer during the session. This may be an article about YouTube, but you should definitely also engage with your community on other social networks as well. Plus, its a great way to take advantage of multiple platforms and tap into new audiences. Being socially present on multiple networks shows that you are availability and committed to your community.
A couple of ways to grow your community include:
Always make sure to link from one social network to the other. A properly placed CTA in your videos can help you achieve this action.
When releasing a new video, announce it on all your other channels. Plus: don’t forget to add a link to your latest vid.
Create a blog to keep your community interested.
Start a forum to keep the conversation going.
Send out newsletters using Wix Email Marketing to promote your weekly blog, announcements or updates.
10. Spread the word with a killer website
When your primary content is made for YouTube, it’s hard to give your brand another home. Sure, you can share your videos on other social networks, and you should, but a stunning video website should be your YouTube channel’s home away from home. The great advantage of a video website is that you’re the owner of everything on your website. Essentially, you’re not confined to what a social media platform has to offer. Therefore, your site has all the benefits of YouTube without any of the limitations. With Wix Video, you can easily sync your YouTube channel to your site, enabling a smooth integration of your videos into your website. That means, more views on your videos straight from your site. From your site, you have the option to sell your videos, rent them or even set up a monthly subscription plan. Best of all, it’s all free.
make-up brand website designmake-up brand website design
11. Learn from your analytics
Even the best can do it better. YouTube offers up a dedicated analytics section for your channel so you can see how your videos are performing. Analytics will allow you to get insight on the people who are watching your videos, which allows you to hone into your target demographic even further. It will also give you a better idea as to why one video may have performed better than another. Basically, it’s a powerful tool you should take advantage of for your budding channel.
10. Spread the word with a killer website
When your primary content is made for YouTube, it’s hard to give your brand another home. Sure, you can share your videos on other social networks, and you should, but a stunning video website should be your YouTube channel’s home away from home. The great advantage of a video website is that you’re the owner of everything on your website. Essentially, you’re not confined to what a social media platform has to offer. Therefore, your site has all the benefits of YouTube without any of the limitations. With Wix Video, you can easily sync your YouTube channel to your site, enabling a smooth integration of your videos into your website. That means, more views on your videos straight from your site. From your site, you have the option to sell your videos, rent them or even set up a monthly subscription plan. Best of all, it’s all free.
make-up brand website designmake-up brand website design
11. Learn from your analytics
Even the best can do it better. YouTube offers up a dedicated analytics section for your channel so you can see how your videos are performing. Analytics will allow you to get insight on the people who are watching your videos, which allows you to hone into your target demographic even further. It will also give you a better idea as to why one video may have performed better than another. Basically, it’s a powerful tool you should take advantage of for your budding channel.
Subscribe to:
Posts (Atom)